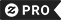Tap / click on image to see more RealViewsTM
$45.45
per shirt
Golden Spiral and Fibonacci Spiral T-Shirt
Qty:
Style
Basic T-Shirt
+$1.80
-$2.15
+$15.15
Colour & Print Process
White
Classic Printing: No Underbase
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
+$1.80
Vivid Printing: White Underbase
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
+$9.00
About T-Shirts
Sold by
About This Design
Golden Spiral and Fibonacci Spiral T-Shirt
The Golden Spiral (back design) is constructed by repeatedly dividing Golden Rectangles in half. A rectangle with proportions such that when divided in half (parallel to a short side) each half has the same proportions, is a Golden Rectangle, and the ratio of a long side to a short side is the Golden Ratio (1.61803398874989484820458683436564). To make a Golden Spiral, divide a Golden Rectangle in half, then divide one of the halves in half, and repeat as long as you like. Which half is divided next is chosen so that diagonals can be drawn across successively smaller rectangles so that these diagonals form a spiral. The Fibonacci Spiral (front design) is constructed by diagonals across squares. The sizes of the squares are determined by the Fibonacci series 1, 1, 2, 3, 5, 8, 13, 21.. where each integer is the sum of the two previous integers. Instead of constructing the spiral from the outside in as for the Golden Spiral, we construct this spiral from the inside out. We start with two squares of size 1 (the length of a side). We can place one square against the other neatly because the sides have the same length. Two other sides are colinear (lie on one line) with a combined length of 2. We place a square of size 2 against this combined length. Then we place diagonals on the three squares such that the diagonals lie end-to-end, making the beginning of the spiral. Now we find two colinear sides of lengths 1 and 2 that touch the longest diagonal, and we place a square of size 3 against this combined length and add another diagonal to the spiral. As we repeat this procedure, we graphically produce the Fibonacci series. The Fibonacci series is related to the Golden Ratio because ratios of adjacent values of the Fibonacci series are increasingly better approximations of the Golden Ratio: 21/13=1.6153, 34/21=1.6190, 55/34=1.6176, etc.
Store
Customer Reviews
4.7 out of 5 stars rating31.9K Total Reviews
31,903 Reviews
Reviews for similar products
5 out of 5 stars rating
By Stuart B.28 June 2025 • Verified Purchase
Basic Dark T-Shirt, Black, Adult L
Excellent design platform, great quality material and printing, and quick delivery: couldn't ask for more...
5 out of 5 stars rating
By Shelley M.3 October 2022 • Verified Purchase
Value T-Shirt, White, Adult L
Zazzle Reviewer Program
I was really pleased with this shirt, the quality of the Tshirt was excellent, the artwork and print stands out and the fit is true to size....my son loved this for his 16th birthday 😀. Very good quality and color
5 out of 5 stars rating
By Vivienne C.9 June 2023 • Verified Purchase
Basic T-Shirt, White, Adult S
Zazzle Reviewer Program
AAA+++ Perfect gift for my old dad. He loved it - highly recommend and will buy again. Printing looked perfect to me
Tags
Other Info
Product ID: 235765739168422667
Posted on 1/11/2005, 6:35 PM
Rating: G
Recently Viewed Items